The formula for the volume of a cylinder is: V = Π x r^2 x h. “Volume equals pi times radius squared times height.” Now you can solve for the radius: V = Π x r^2 x h <– Divide both sides by Π x h to get: V / (Π x h) = r^2 <– Square root both sides to get: sqrt (V / Π x h) = r. 3 comments.
Primary Maths 3D view of Objects Cone, Pyramid, Cylinder, Sphere on Cuboid JavaScript Model Simulation Applet HTML5 – Open Educational Resources / Open Source Physics @ Singapore | Open Educational Resources / Open Source Physics @ Singapore
The cylinder and the sphere below have the same radius and the same volume. What is the height of the cylinder? 6m 6m Veylinder = Tr²h Vsphere = r Algebra & Trigonometry with Analytic Geometry 13th Edition ISBN: 9781133382119 Author: Swokowski Publisher: Swokowski Chapter4: Polynomial And Rational Functions Section4.3: Zeros Of Polynomials
Source Image: hkdivedi.com
Download Image
Nov 21, 2023A sphere inside a cylinder, where both have the same radii. As shown in the figure above, the height of the cylinder will be twice the radius, that is, eqh=2r /eq

Source Image: blenderartists.org
Download Image
The sphere and the cylinder – part 1 – SSDD Problems The formula for the volume of a cylinder is V = π(r)^2(h), and the formula for the volume of a sphere is V = (4/3)π(r)^3. Since we know the cylinder has a height of 8, we can substitute this value in for h. Since the volumes of the two figures are equal to each other, we can set the two equations equal to each other. In other words:
Source Image: hkdivedi.com
Download Image
The Cylinder And The Sphere Below Have The Same
The formula for the volume of a cylinder is V = π(r)^2(h), and the formula for the volume of a sphere is V = (4/3)π(r)^3. Since we know the cylinder has a height of 8, we can substitute this value in for h. Since the volumes of the two figures are equal to each other, we can set the two equations equal to each other. In other words: VIDEO ANSWER: The height and radius are clinical. The amount of a cylinder is five. Our square feet are large. The value of age is square minus of argued. Are we going to find the maximum value of the DVD? There will be by 24 are -3 R Squared. Okay,
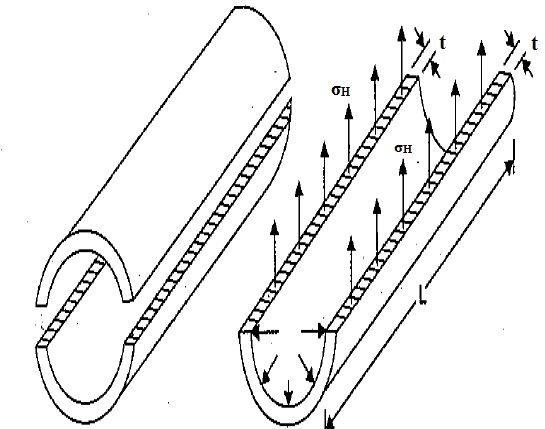
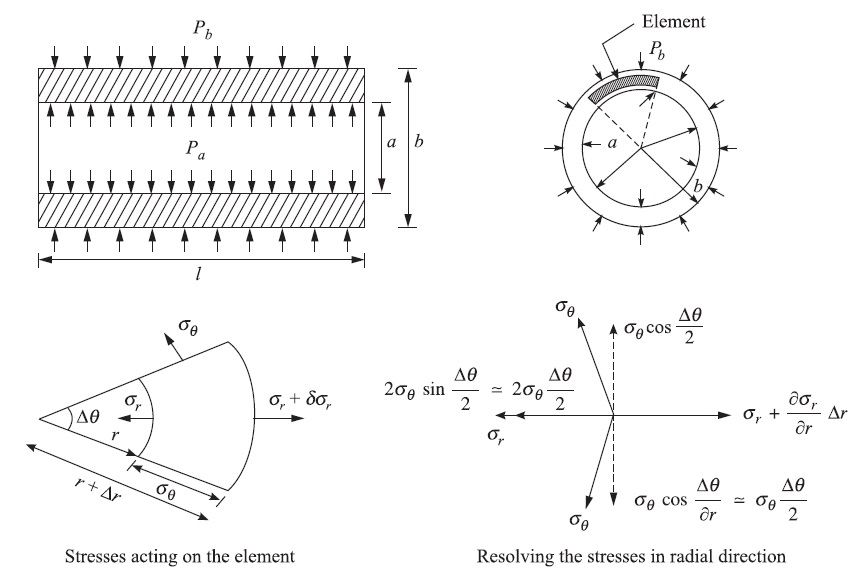
THICK CYLINDER LAME’S EQUATION – ENGINEERING APPLICATIONS
the result for the relationship between the volumes of a sphere, a cone and a cylinder was allegedly established by Archimedes using small slices. this is explained in ‘Cut the Knot’ and illustrated here. it can be shown that the volume of the thin disk is the same as the volume of the ring. there’s an illustration (with the above diagram) with Waste Management in Spinning

Source Image: textilesphere.com
Download Image
MEDIAN Don Steward mathematics teaching: cone, sphere, cylinder the result for the relationship between the volumes of a sphere, a cone and a cylinder was allegedly established by Archimedes using small slices. this is explained in ‘Cut the Knot’ and illustrated here. it can be shown that the volume of the thin disk is the same as the volume of the ring. there’s an illustration (with the above diagram) with
Source Image: donsteward.blogspot.com
Download Image
Primary Maths 3D view of Objects Cone, Pyramid, Cylinder, Sphere on Cuboid JavaScript Model Simulation Applet HTML5 – Open Educational Resources / Open Source Physics @ Singapore | Open Educational Resources / Open Source Physics @ Singapore The formula for the volume of a cylinder is: V = Π x r^2 x h. “Volume equals pi times radius squared times height.” Now you can solve for the radius: V = Π x r^2 x h <– Divide both sides by Π x h to get: V / (Π x h) = r^2 <– Square root both sides to get: sqrt (V / Π x h) = r. 3 comments.
Source Image: iwant2study.org
Download Image
The sphere and the cylinder – part 1 – SSDD Problems Nov 21, 2023A sphere inside a cylinder, where both have the same radii. As shown in the figure above, the height of the cylinder will be twice the radius, that is, eqh=2r /eq

Source Image: ssddproblems.com
Download Image
SOLVED: A cylinder, cone, and sphere are shown below. The three figures have the same radius. The cylinder and cone have the same height with h = r. If the volume of The cylinder and the sphere below have the same radius and the same volume. What is the height of the cylinder? Some {and the sphere below have the same radius and the same volume e cylinder? Vcylinder = πr^2h Vsphere = (4/3)πr^3 8m 6m 4m. Instant Answer:
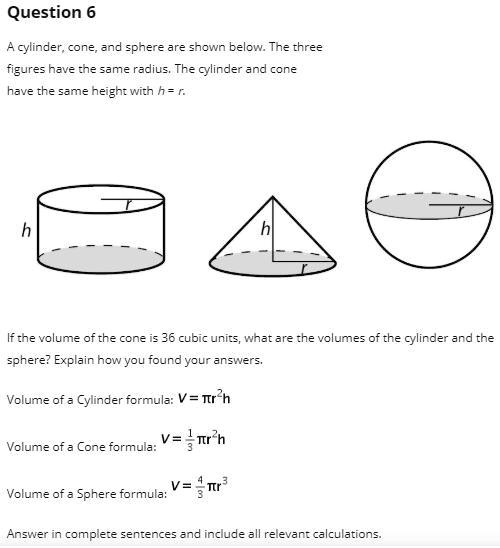
Source Image: numerade.com
Download Image
Teaching Flat Plane Shapes & Solid Shapes | Houghton Mifflin Harcourt The formula for the volume of a cylinder is V = π(r)^2(h), and the formula for the volume of a sphere is V = (4/3)π(r)^3. Since we know the cylinder has a height of 8, we can substitute this value in for h. Since the volumes of the two figures are equal to each other, we can set the two equations equal to each other. In other words:

Source Image: hmhco.com
Download Image
Mrs. Newell’s Math: #MTBoS30: Cones, Cylinders, & Spheres VIDEO ANSWER: The height and radius are clinical. The amount of a cylinder is five. Our square feet are large. The value of age is square minus of argued. Are we going to find the maximum value of the DVD? There will be by 24 are -3 R Squared. Okay,

Source Image: newellssecondarymath.blogspot.com
Download Image
MEDIAN Don Steward mathematics teaching: cone, sphere, cylinder
Mrs. Newell’s Math: #MTBoS30: Cones, Cylinders, & Spheres The cylinder and the sphere below have the same radius and the same volume. What is the height of the cylinder? 6m 6m Veylinder = Tr²h Vsphere = r Algebra & Trigonometry with Analytic Geometry 13th Edition ISBN: 9781133382119 Author: Swokowski Publisher: Swokowski Chapter4: Polynomial And Rational Functions Section4.3: Zeros Of Polynomials
The sphere and the cylinder – part 1 – SSDD Problems Teaching Flat Plane Shapes & Solid Shapes | Houghton Mifflin Harcourt The cylinder and the sphere below have the same radius and the same volume. What is the height of the cylinder? Some {and the sphere below have the same radius and the same volume e cylinder? Vcylinder = Ï€r^2h Vsphere = (4/3)Ï€r^3 8m 6m 4m. Instant Answer: