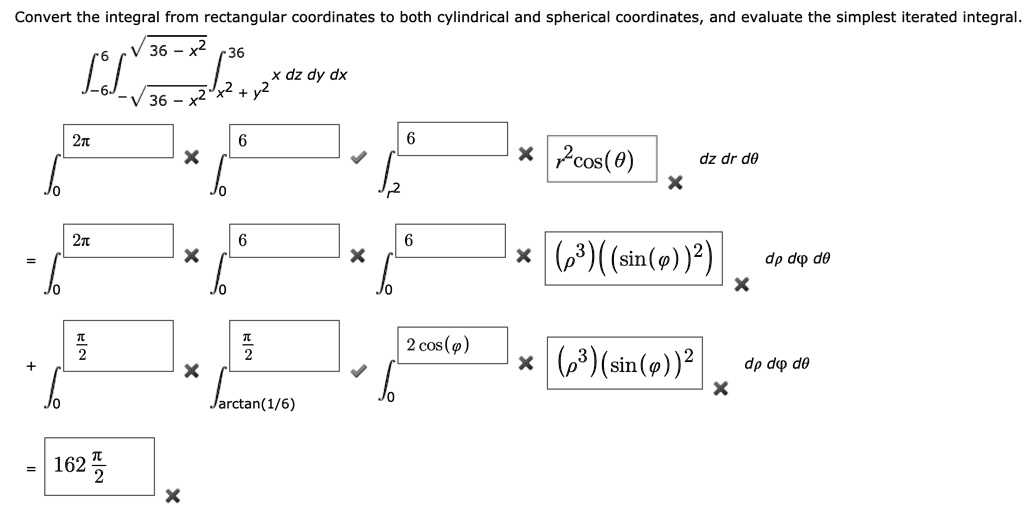
Integration in Cylindrical Coordinates Definition. Cylindrical coordinates represent a point P in space by the ordered triple (r,θ,z)where 1. r and θ are the polar coordinates for the vertical projection of P onto the xy-plane. 2. z is the rectangular vertical coordinate of P. x y z b b P(r,θ,z) The following equations relate rectangular
15.7: Triple Integrals in Cylindrical Coordinates – YouTube
1 Evaluate the following integrals. a) Z π 0 Z 2 0 Z 9−r2 0 r dzdrdθ b) Z 2π 0 Z π π/2 Z 2 1 ρ2sinφ dρdφdθ 2 Use cylindrical coordinates to find the volume of the solid that lies within both the cylinder x2+y2 = 1 and the sphere x2+y2+z2 = 4. 3 Use spherical coordinates to evaluate Z Z Z H (16−x2−y2)dV , where H is the solid

Source Image: chegg.com
Download Image
Expanding the tiny unit of volume d V in a triple integral over cylindrical coordinates is basically the same, except that now we have a d z term: ∭ R f ( r, θ, z) d V = ∭ R f ( r, θ, z) r d θ d r d z. Remember, the reason this little r shows up for polar coordinates is that a tiny “rectangle” cut by radial and circular lines has side
Source Image: numerade.com
Download Image
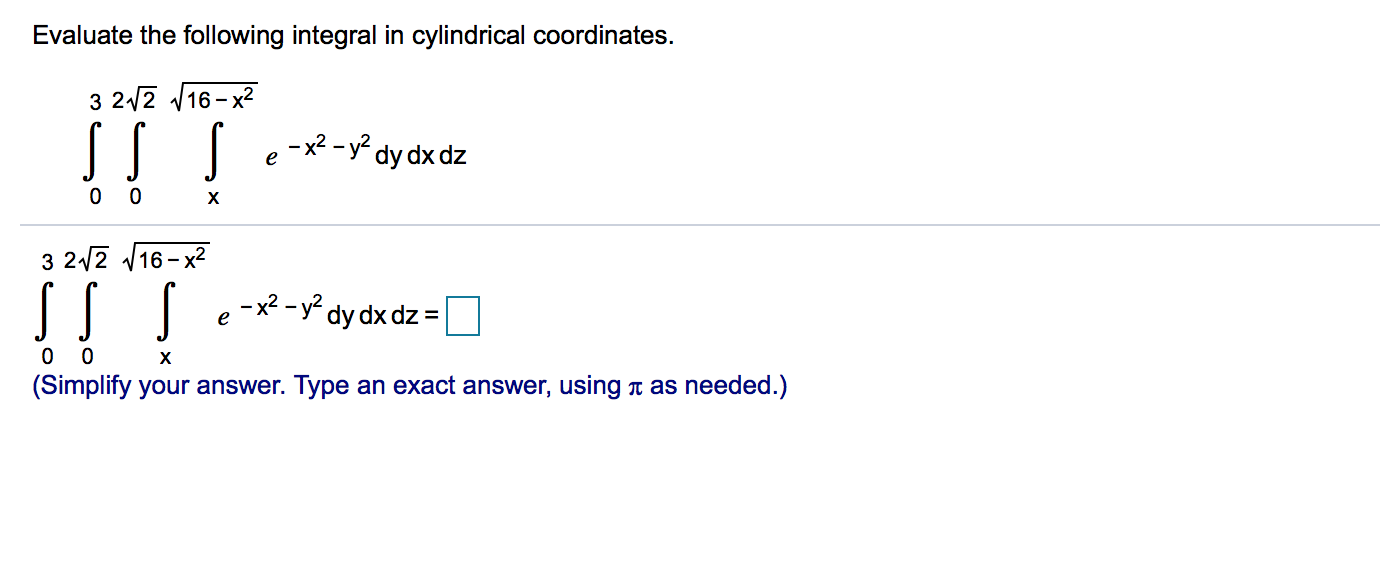
Solved Evaluate the integral by changing to cylindrical | Chegg.com Get the free “Triple Integral – Cylindrical” widget for your website, blog, WordPress, Blogger, or iGoogle. Find more Mathematics widgets in Wolfram|Alpha.

Source Image: study.com
Download Image
Evaluate The Following Integral In Cylindrical Coordinates.
Get the free “Triple Integral – Cylindrical” widget for your website, blog, WordPress, Blogger, or iGoogle. Find more Mathematics widgets in Wolfram|Alpha. 2. Evaluate the triple integral in spherical coordinates. f(x;y;z) = 1=(x2 + y2 + z2)1=2 over the bottom half of a sphere of radius 5 centered at the origin. 3. For the following, choose coordinates and set up a triple integral, inlcluding limits of integration, for a density function fover the region. (a)
Cylindrical & Spherical Coordinates | Conversion & Examples – Video & Lesson Transcript | Study.com
Nov 16, 2022Evaluate the following integral by first converting to an integral in cylindrical coordinates. ∫ √5 0 ∫ 0 −√5−x2∫ 9−3×2−3y2 x2+y2−11 2x −3y dzdydx ∫ 0 5 ∫ − 5 − x 2 0 ∫ x 2 + y 2 − 11 9 − 3 x 2 − 3 y 2 2 x − 3 y d z d y d x Solution Solved Evaluate the following integral in cylindrical | Chegg.com

Source Image: chegg.com
Download Image
Solved Evaluate the following integral in cylindrical | Chegg.com Nov 16, 2022Evaluate the following integral by first converting to an integral in cylindrical coordinates. ∫ √5 0 ∫ 0 −√5−x2∫ 9−3×2−3y2 x2+y2−11 2x −3y dzdydx ∫ 0 5 ∫ − 5 − x 2 0 ∫ x 2 + y 2 − 11 9 − 3 x 2 − 3 y 2 2 x − 3 y d z d y d x Solution
Source Image: chegg.com
Download Image
15.7: Triple Integrals in Cylindrical Coordinates – YouTube Integration in Cylindrical Coordinates Definition. Cylindrical coordinates represent a point P in space by the ordered triple (r,θ,z)where 1. r and θ are the polar coordinates for the vertical projection of P onto the xy-plane. 2. z is the rectangular vertical coordinate of P. x y z b b P(r,θ,z) The following equations relate rectangular
Source Image: m.youtube.com
Download Image
Solved Evaluate the integral by changing to cylindrical | Chegg.com Expanding the tiny unit of volume d V in a triple integral over cylindrical coordinates is basically the same, except that now we have a d z term: ∭ R f ( r, θ, z) d V = ∭ R f ( r, θ, z) r d θ d r d z. Remember, the reason this little r shows up for polar coordinates is that a tiny “rectangle” cut by radial and circular lines has side
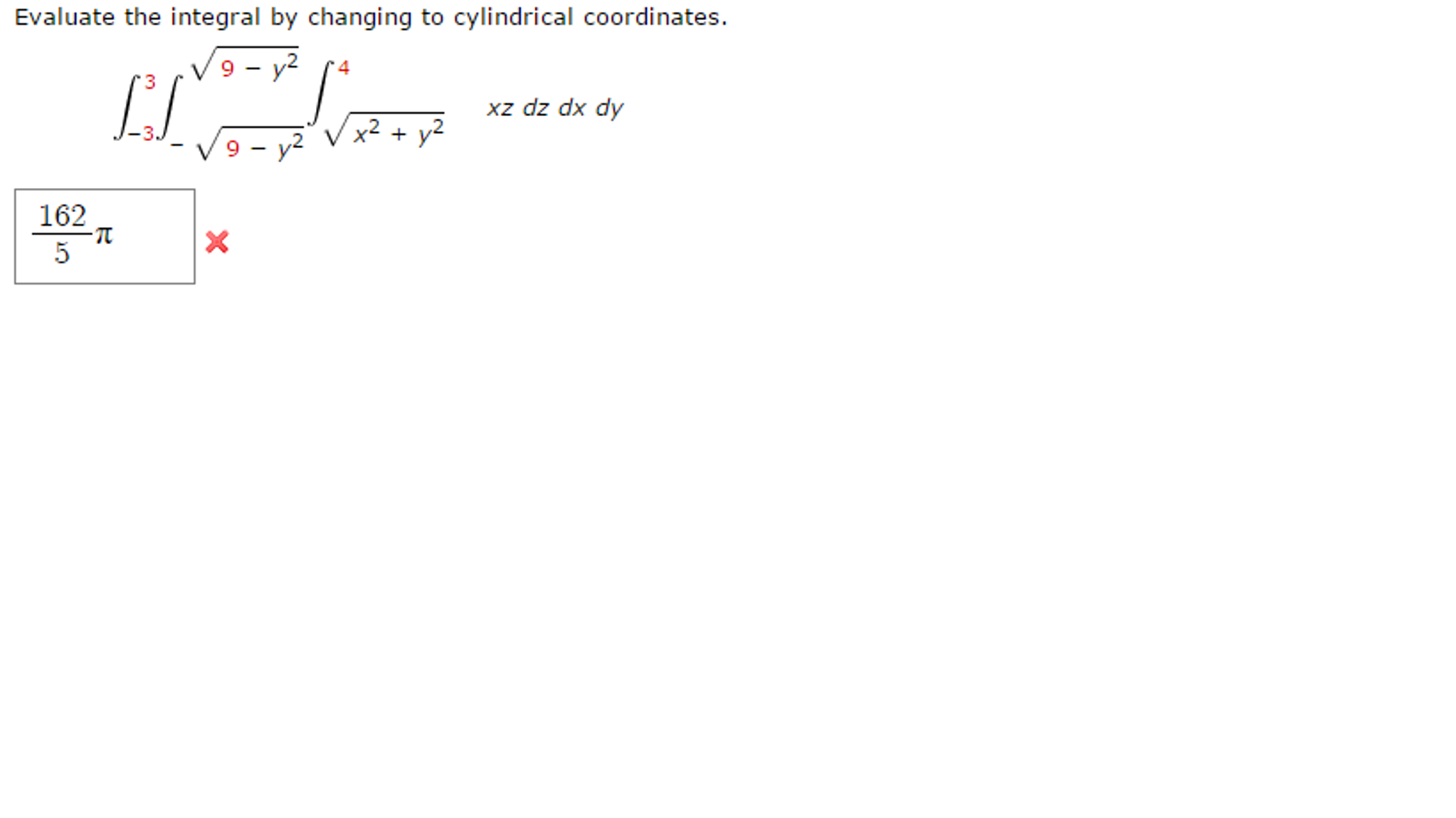
Source Image: chegg.com
Download Image
Answered: Evaluating Integrals in Cylindrical… | bartleby Feb 27, 2022Stage 2. 6. Use cylindrical coordinates to evaluate the volumes of each of the following regions. Above the xy –plane, inside the cone z = 2a − √x2 + y2 and inside the cylinder x2 + y2 = 2ay. Above the xy –plane, under the paraboloid z = 1 − x2 − y2 and in the wedge − x ≤ y ≤ √3x.

Source Image: bartleby.com
Download Image
Evaluate the integral by changing to cylindrical coordinates | Quizlet Get the free “Triple Integral – Cylindrical” widget for your website, blog, WordPress, Blogger, or iGoogle. Find more Mathematics widgets in Wolfram|Alpha.
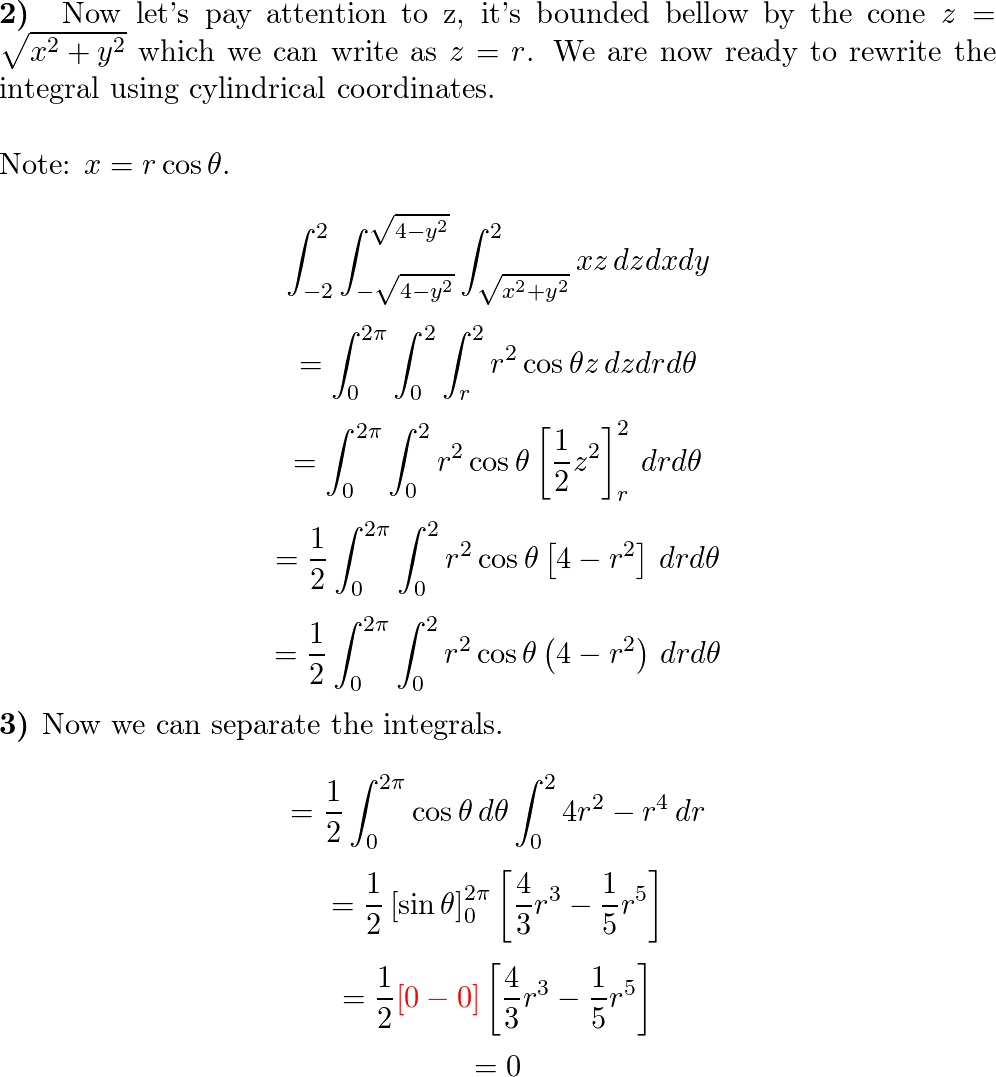
Source Image: quizlet.com
Download Image
Answered: Evaluate the integral by changing to… | bartleby 2. Evaluate the triple integral in spherical coordinates. f(x;y;z) = 1=(x2 + y2 + z2)1=2 over the bottom half of a sphere of radius 5 centered at the origin. 3. For the following, choose coordinates and set up a triple integral, inlcluding limits of integration, for a density function fover the region. (a)

Source Image: bartleby.com
Download Image
Solved Evaluate the following integral in cylindrical | Chegg.com
Answered: Evaluate the integral by changing to… | bartleby 1 Evaluate the following integrals. a) Z π 0 Z 2 0 Z 9−r2 0 r dzdrdθ b) Z 2π 0 Z π π/2 Z 2 1 ρ2sinφ dρdφdθ 2 Use cylindrical coordinates to find the volume of the solid that lies within both the cylinder x2+y2 = 1 and the sphere x2+y2+z2 = 4. 3 Use spherical coordinates to evaluate Z Z Z H (16−x2−y2)dV , where H is the solid
Solved Evaluate the integral by changing to cylindrical | Chegg.com Evaluate the integral by changing to cylindrical coordinates | Quizlet Feb 27, 2022Stage 2. 6. Use cylindrical coordinates to evaluate the volumes of each of the following regions. Above the xy –plane, inside the cone z = 2a − √x2 + y2 and inside the cylinder x2 + y2 = 2ay. Above the xy –plane, under the paraboloid z = 1 − x2 − y2 and in the wedge − x ≤ y ≤ √3x.